Bagian dari turunan material 1Persamaan 4.52 yang diwakili oleh turunan spasial disebut turunan konvektif. Ini menggambarkan fakta bahwa sebuah sifat aliran yang terkait dengan sebuah partikel fluida dapat bervariasi karena pergerakan partikel dari satu titik dalam ruang di mana parameter memiliki satu nilai ke titik lain dalam ruang di mana nilainya berbeda. Sebagai contoh, kecepatan air di inlet nozzle selang kebun yang ditunjukkan dalam gambar di pinggir halaman berbeda (baik dalam arah maupun kecepatan) dibandingkan dengan di outlet. Kontribusi ini terhadap laju perubahan parameter untuk partikel dapat terjadi apakah aliran itu mantap atau tidak mantap.
Ini disebabkan oleh adveksi, atau pergerakan, partikel melalui ruang di mana terdapat gradien [∇( )=𝜕( )/𝜕𝑥 𝑖+𝜕( )/𝜕𝑦 𝑗+𝜕( )/𝜕𝑧 𝑘] dalam nilai parameter. Bagian dari percepatan yang diberikan oleh istilah (V = ∇)V disebut sebagai percepatan advektif.
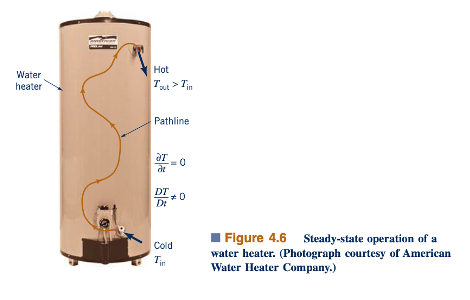
Seperti yang diilustrasikan dalam Gambar 4.6, suhu partikel air berubah saat mengalir melalui pemanas air. Air yang memasuki pemanas selalu memiliki suhu dingin yang sama, dan air yang keluar dari pemanas selalu memiliki suhu panas yang sama. Aliran adalah mantap. Namun, suhu, T, dari setiap partikel air meningkat saat melewati pemanas — Tout > Tin. Oleh karena itu, DT/Dt ≠ 0 tidak sama dengan 0 karena adanya suku konvektif dalam turunan total suhu. Artinya, 𝜕T/𝜕t = 0, tetapi u 𝜕T/𝜕x ≠ 0 (di mana x diarahkan sepanjang garis arus), karena terdapat gradien suhu yang tidak nol sepanjang garis arus. Partikel fluida yang bergerak sepanjang jalur suhu yang tidak konstan ini (di mana 𝜕T/𝜕x ≠ 0) pada kecepatan tertentu (u) akan mengalami perubahan suhu seiring waktu pada laju DT/Dt = u 𝜕T/𝜕x meskipun alirannya mantap (𝜕T/𝜕t=0).
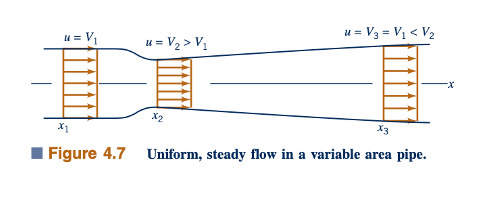
Proses yang sama terlibat dalam percepatan fluida. Pertimbangkan aliran dalam pipa dengan luas yang bervariasi seperti yang ditunjukkan dalam Gambar 4.7. Diasumsikan bahwa aliran tersebut mantap dan satu dimensi dengan kecepatan yang meningkat dan menurun sepanjang arah aliran seperti yang ditunjukkan. Saat fluida mengalir dari bagian (1) ke bagian (2), kecepatannya meningkat dari V1 ke V2 . Oleh karena itu, meskipun 𝜕V/𝜕t = 0 (aliran mantap), partikel fluida mengalami percepatan yang diberikan oleh a = u(𝜕u/𝜕x) (percepatan konvektif). Untuk x1 ≤ x ≤ x2, terlihat bahwa 𝜕u/𝜕x > 0 sehingga ax > 0 — fluida mempercepat. Untuk x2 ≤ x ≤ x3, terlihat bahwa 𝜕u/𝜕x < 0 sehingga ax < 0 — fluida melambat. Percepatan dan perlambatan ini ditunjukkan dalam gambar di pinggir. Jika V1 = V3, jumlah percepatan secara tepat seimbang dengan jumlah perlambatan meskipun jarak antara x2 dan x1 serta x3 dan x2 tidak sama.
Konsep turunan material dapat digunakan untuk menentukan laju perubahan waktu dari setiap parameter yang terkait dengan sebuah partikel saat bergerak. Penggunaannya tidak terbatas pada mekanika fluida saja. Bahan dasar yang diperlukan untuk menggunakan konsep turunan material adalah deskripsi lapangan parameter, P = P(x, y, z, t), dan laju pergerakan partikel melalui lapangan tersebut, V = V (x, y, z, t).